progressão mista é a sequência numérica 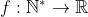 , onde
, onde
Cada termo, a partir do segundo, é igual ao anterior vezes uma constante  e mais uma constante
e mais uma constante  , ou seja
, ou seja
Ou então, cada termo, a partir do segundo, é igual ao anterior mais uma constante  e vezes uma constante
e vezes uma constante  , ou seja,
, ou seja,
As constantes  e
e  ( ou
( ou  ) são denominadas razão multiplicativa e aditiva da progressão mista, respectivamente.
) são denominadas razão multiplicativa e aditiva da progressão mista, respectivamente.
O segundo conceito é equivalente ao primeiro, pois temos
Logo, para cada  onde
onde 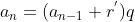 , existirá um
, existirá um  tal que
tal que 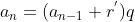 . De fato, pois
. De fato, pois 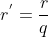 .
.
Adotaremos a primeira definição com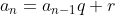 .
.
Adotaremos a primeira definição com
Exemplo
Sejam 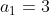 ,
, 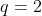 e
e 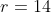 .
.
Formaremos os quatro primeiros termos da progressão mista de duas formas: com
Cálculo das razões  e
e 
Do sistema
tiramos
com
( fornecida pela primeira equação do sistema )
Assim, precisamos de três termos consecutivos 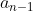 ,
, 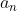 e
e 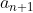 para acharmos as razões
para acharmos as razões  e
e  da progressão mista.
da progressão mista.
Calcular as razões da progressão mista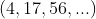 . Temos, então,
. Temos, então, 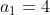 ,
, 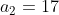 e
e 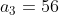 . Logo,
. Logo,
Exemplo
Calcular as razões da progressão mista
Sendo possível estes cálculos, concluímos que, dados três números quaisquer que não estejam em 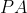 ou
ou 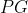 , então estes números sempre farão parte de uma progressão mista.
, então estes números sempre farão parte de uma progressão mista.
Pela relação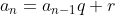 , temos
, temos
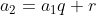
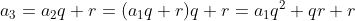
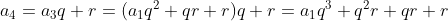
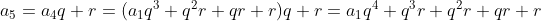
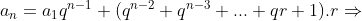
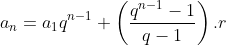
Fórmula do termo geral
Pela relação
................................................................................................................................................
Exemplos
Assim, a sequência do primeiro exemplo 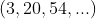 , com
, com 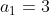 ,
,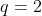 e
e 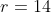 fica
fica
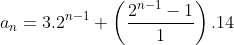
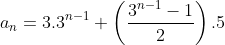
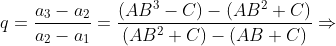
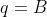
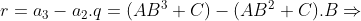

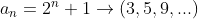 , com
, com 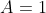 ,
, 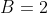 e
e 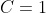
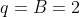
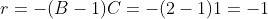
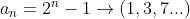 , com
, com 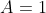 ,
, 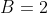 e
e 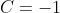
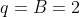
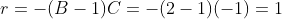
Enquanto que a sequência do segundo exemplo 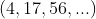 , com
, com 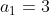 ,
, 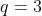 e
e 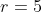 tem a forma
tem a forma
Considerações sobre o termo geral - forma sintética
Com um pequeno rearranjo, a fórmula 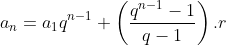 se transforma em
se transforma em
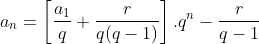
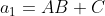 ,
, 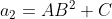 e
e 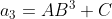
e chegamos a forma sintética 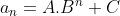 , com
, com
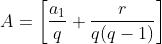 ,
, 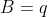 e
e 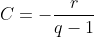
Na forma sintética, temos
Assim,
Exemplos 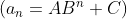
Curiosidades
A fórmula que fornece a soma dos  primeiros termos de uma progressão geométrica (
primeiros termos de uma progressão geométrica (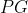 ), de primeiro termo
), de primeiro termo 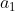 e razão
e razão 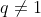 , ou seja,
, ou seja, 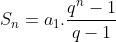 , é o enésimo termo de uma progressão mista. De fato,
, é o enésimo termo de uma progressão mista. De fato,
com 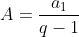 ,
, 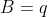 e
e 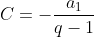 , sendo
, sendo
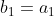
A sequência constante
Sugestão de pesquisa
Referência bibliográfica: Coleção Fundamentos de Matemática Elementar-V4.
Imagem: http://www.fractal.org/Fractal-tree-scaffold.htm

